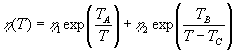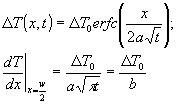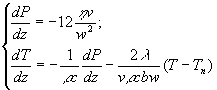Рассмотрено движение однофазной вязкой магмы по щели постоянного сечения. Вязкость магмы описана двучленной формулой, учитывающей резкое возрастание вязкости вблизи точки замерзания магмы и плавное уменьшение вязкости в области высоких температур. Составлена система уравнений, описывающих движение магмы с учетом вязкого нагрева и теплопотерь через стенки щели. Задачи решены на ЭВМ для широкого диапазона начальных условий в питающем очаге. На основании результатов решения получено приближенное аналитическое соотношение, связывающее главные параметры задачи (глубину залегания Н питающего очага, избыточное давление Р и температуру То магмы в нем, толщину W и время существования t дайки, а также скорость v движения магмы по дайке). Определены границы стабильного движения магмы. Получена приближенная формула, связывающая предельные параметры Vmin и pmin (минимальную скорость стабильного движения и давление, при котором движение магмы прекращается) с параметрами дайки и питающего очага.
Вулканические извержения делятся на извержения центрального (из одного или нескольких жерл или кратеров) типа и трещинного типа. Во время последних лава, вулканический шлак, пепел и газы извергаются из протяженных трещин, раскрывающихся на поверхности суши или дна морей и океанов. Огромные напластования базальтов в областях развития траппового вулканизма и в срединных океанических хребтах образовались вследствие трещинных извержений. Трещинные извержения происходят на склонах крупных базальтовых вулканов. Алмазоносные вулканические взрывные трубки переходят на глубине в трещины, образовавшиеся при внедрении магмы. Трещинные вулканические извержения и вызывающая их магматическая деятельность являются важными, распространенными геологическими явлениями, механизм которых еще слабо изучен. Задача интересна и в прикладном отношении, так как многочисленные базальтовые дайки могут быть источником тепла во многих геотермальных месторождениях, а ее исследование необходимо для выяснения того, каким образом алмазы выносятся из глубин Земли.
Общей особенностью трещинных и многих других вулканических извержений является то, что они имеют более или менее продолжительную стадию, при которой жидкая магма с больших глубин поднимается по трещине к поверхности Земли. Иногда эта трещина (дайка) доходит до самой поверхности, иногда она оканчивается одним или несколькими каналами круглого сечения - трубками, или жерлами. Целесообразно проследить, как происходит этот подъем, какие закономерности им управляют. Поскольку экспериментальные исследования в этой области затруднены и ненадежны как для действующих вулканов, так и для обнажений застывших даек прошлых извержений, то явную ценность представляли бы попытки математического моделирования процесса подъема магмы по дайке. Они предпринимались и ранее: вязкий разогрев и вызванное им ускорение магмы рассматривались в [1], краткий обзор и анализ задачи проведены в [2], в [3] приводится упрощенное уравнение теплового баланса и скорости течения магмы в дайке, более общее решение получено в [4].
Цель настоящей работы - исследование взаимосвязи основных параметров, определяющих процесс течения магмы по дайкам; основной инструмент исследования — математическое моделирование процесса. Очевидно, ценность результатов моделирования тем выше, чем больше достоверных особенностей подъема магмы заложено в модель. Однако пропорционально этому возрастают и математические трудности. В настоящей работе задача значительно упрощена. Исходные предпосылки для расчета таковы:
1. Магма характеризуется температурой затвердевания Тс, вязкость ее h описывается формулой
|
|
(1) |
Такая двучленная формула вязкости выбрана из тех соображений, чтобы ею можно было пользоваться при всех температурах Т > Тс. Численные значения констант h1, h2, ТА, ТВ и ТС были подобраны по наилучшему совпадению функциональной зависимости (1) с известными экспериментальными данными для свободно изливающихся лав Вообще говоря, наибольшего соответствия формулы (1) реальным магмам следует ожидать для вулканов гавайского типа с малым содержанием летучих. Данные по вязкости лав вулканов стромболианского типа (и тем более типов, характеризующихся еще большей эксплозивной активностью) в данном случае ненадежны, так как на больших глубинах вязкость магмы существенно отличается от вязкости в наземных лавовых потоках. Из сопоставления с литературными данными [5, 6] для констант формулы вязкости выбраны следующие величины: h 1= 2,75; h 2 = 150; ТА = 6800 К; ТВ = 600 К; ТС = 1250 К. Графически функция (1) изображена на рис. 1.
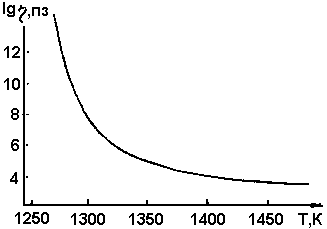
Рис. 1. Температурная зависимость вязкости магмы.
2. Движущей силой, поднимающей магму по дайке, является избыточное гидростатическое давление в магматическом очаге (выталкивающая сила Архимеда). Величина этого давления определяется вертикальным размером магматического очага (или колонны, питающей очаг) и разницей плотностей магмы и вмещающих пород. Рассматривается диапазон избыточных давлений от 105 до 109 Па.
3. Температура породы возрастает с глубиной по закону, определяемому табл. 1 [6 - 8]. Разные авторы дают существенно различающиеся значения геотермических градиентов, и это не случайно, поскольку в различных районах Земли геотермы действительно меняются в широких пределах (кроме всего прочего, надежность почти всех сведений о свойствах глубинных слоев пока оставляет желать лучшего). К счастью, результат моделирования подъема магмы по дайке практически совершенно нечувствителен к форме геотермы. Гораздо более важным является тот факт, что на начальном участке дайки (первые ~10% ее длины) прогрев пород магматическим очагом повышает температуру пород. Можно полагать, что на этих глубинах температура спадает линейно от температуры в очаге до температуры, определяемой геотермическим градиентом согласно табл. 1.
Таблица 1.
|
Глубина, км |
Область |
|||||||
|
Континент |
Островные дуги |
Океанское дно |
||||||
|
[6] |
[7] |
[8] |
[6] |
[8] |
[6] |
[7] |
[8] |
|
|
0 |
200 |
300 |
273 |
300 |
273 |
300 |
273 |
273 |
|
11 |
- |
- |
- |
- |
- |
- |
404 |
- |
|
20 |
- |
653 |
- |
- |
- |
- |
- |
- |
|
35 |
673 |
- |
- |
773 |
- |
773 |
- |
- |
|
40 |
- |
923 |
- |
- |
- |
- |
1123 |
- |
|
50 |
- |
973 |
973 |
- |
1373 |
- |
1373 |
1373 |
|
70 |
950 |
- |
- |
1023 |
- |
1073 |
- |
- |
4. Дайка вертикальна, т.е. в ней нет участков с резким изменением направления. (Плавные изменения для расчета несущественны, просто в этом случае следует оперировать полной длиной дайки, а не кратчайшим расстоянием от очага до поверхности.)
5. При движении по дайке с холодными стенками в магме происходят два конкурирующих процесса: охлаждение за счет теплоотдачи стенкам и подогрев за счет работы против сил вязкого трения (Считается, что вязкий разогрев обычно является более слабым эффектом [4,9]).
6. Поперечное сечение дайки постоянно по всей длине.
7. Температура и скорость магмы постоянны по сечению дайки. В действительности постоянство Т и v не выполняется ни при каких режимах течения. Оценки показывают, что во всех режимах, близких к реальным, течение магмы по дайке ламинарно, в этом случае распределение скорости по сечению щели подчиняется параболическому закону [10]. Краевой эффект имеет место и на границах щели, однако здесь достаточно вспомнить, что ширина дайки обычно значительно больше ее толщины, т.е. влияние краев несущественно. Что касается распределения скорости по толщине, то можно без большой погрешности заменить параболическое распределение плоским, при этом эффективная средняя скорость v = 2/3vmax (vmax - скорость на оси потока). Различие температуры магмы в центре дайки и у стенки для даек, время существования которых превышает несколько часов, составляет единицы градусов даже при толщине в несколько метров, так что и в этом случае усреднение по сечению не должно дать значительной ошибки.
8. Магма не изменяет свой объем в процессе подъема. В этом допущении скрыты два условия: несжимаемость (или малая сжимаемость) магмы и отсутствие (или очень малая концентрация) летучих в магме. Сжимаемость магмы могла бы сыграть заметную роль лишь при давлениях > 109 Па, т.е. на глубинах > 30 км [11]; впрочем, этот фактор нетрудно учесть, соответствующим образом изменяя толщину дайки по мере изменения глубины. Выделение летучих из магмы - процесс значительно более важный, поскольку при этом во много раз меняется не только объем магмы (а значит, и ее скорость), но и ее вязкость, причем может меняться и сам характер движения газожидкостной смеси (вулканическое дрожание). Поэтому настоящая модель, вообще говоря, пригодна для описания движения магмы с большим содержанием летучих лишь на глубинах > 1 км (газы начинают отделяться на меньших глубинах). Но если этот последний километр составляет незначительную часть пути магмы от вершины питающего очага до дневной поверхности, то ошибка в определении интегральных характеристик процесса для настоящей модели не должна быть велика.
Учитывая эти упрощения, можно составить систему из двух уравнений, описывающих состояние магмы как функцию высоты z подъема по дайке. Толщина w дайки и ее ширина L постоянны, так что при постоянном объемном расходе Q линейная скорость магмы тоже постоянна. Таким образом, переменными величинами в нашей задаче остаются температура Т магмы и избыточное давление Р. Обе они являются функцией координаты z.
Рассмотрим элемент дайки высотой dz. Перепад избыточного давления dP на верхнем и нижнем сечениях элемента обусловлен вязким трением. Известно [12], что при ламинарном течении в щели ![]() . Других причин, которые вызывали бы изменение избыточного давления, в этой задаче нет, поэтому окончательно для давления получаем
. Других причин, которые вызывали бы изменение избыточного давления, в этой задаче нет, поэтому окончательно для давления получаем
|
|
(2) |
Работа сил избыточного давления целиком переходит в тепло (потенциальная энергия поднимающейся магмы изменяется за счет работы сил абсолютного гидростатического давления в дайке, а работу против сил трения совершает только избыточное давление). Простой анализ размерностей показывает, что изменение температуры магмы за счет вязкого нагрева равно
|
|
(3) |
Однако температура магмы изменяется еще и за счет теплопередачи к холодным стенкам. Очевидно, величина теплопередачи существенно зависит от возраста дайки. Задача математической физики о теплопередаче от тела фиксированной температуры (рассматривается квазистационарный режим) к стенке, начальная температура которой также имела заданную величину, решается в аналитическом виде. При начальной разности температур DТ0 и известных теплопроводности l , плотности r и теплоемкости с вещества стенки решение выглядит так:
|
|
(4) |
где ![]() - коэффициент температуропроводности стенки
- коэффициент температуропроводности стенки ![]() .
.
Следует учесть, что возраст различных участков дайки неодинаков. Если с момента выхода магмы на поверхность прошло время t0 и магма все это время двигалась со скоростью v, то для глубины h возраст дайки будет равен
|
|
(5) |
Переходя от dT/dx к dT/dz, при квазистационарном режиме течения для температуры магмы можно записать уравнение
|
|
(6) |
где Тп=Тп(z – температура породы на заданной глубине.
В итоге получаем систему
|
|
(А) |
Заметим, что кроме явных зависимых переменных P(z) и T(z) в уравнении присутствуют и переменная Tп(z), и две неявные переменные:![]() и
и ![]() .
.
Граничные условия задачи определяются следующим образом.
При заданных v, w и t можно фиксировать длину дайки Н (т.е. глубину залегания питающего очага). Тогда, если начало координат (z = 0) поместить в точку истока дайки, то на поверхности (z = Н) разумно считать избыточное давление нулевым: (Р = 0 при z = Н). Второе граничное условие определяется заданием температуры магмы в питающем очаге (Т=Т0 при z=0).
В аналитическом виде систему (А) решить невозможно. Машинное же решение для любых начальных условий не представляет труда. Графики P(z) и dT(z) – почти прямые линии (dT=T-T0 – изменение температуры магмы в процессе подъема).
Процесс подъема магмы в настоящей модели зависит от величин Т0, Н, w, v и t. Поэтому следующим шагом было определение суммарного избыточного давления в очаге РS и суммарного изменения температуры D ТS магмы в виде функции от перечисленных параметров.
Такая задача была решена в следующем диапазоне изменения параметров:
Т0 – от 1300 до 1500К;
Н – от 1 до 60 км;
w - от 1 см до 40 м;
v - от 0,1 мм/с до 30 м/с;
t - от 100 с до 3 лет.
Результат представлен в виде нескольких семейств кривых. Каждое семейство было получено следующим образом: выбирали точку в пятимерном пространстве параметров, т.е. конкретный набор величин T0, H, v, w, t (существует еще и шестой параметр – температура породы, но влияние его очень мало. Расчет показал, что результаты совпадают с точностью не хуже 2% для всех геотерм, представленных в таблице 1), затем две из координат мы изменяли в заданном диапазоне, причем одна переменная пробегала 100 значений (и являлась впоследствии абсциссой графиков), вторая – 10 значений (и являлась на рисунке параметром семейства кривых). Такой обширный объем расчетной работы позволил провести довольно подробный анализ функциональной зависимости PS (T0,H,v,w,t). Наиболее "представительные" семейства кривых показаны на рис. 2-6.
Эти рисунки относятся к "исходной" точке с координатами: v=1 м/с, w=1 м, T0= 1500K, H=10 км, t=3 сут (эта точка отмечена на графиках крестиком). Заметим, что для наглядности качественной картины процесса решение рассматривается в диапазоне избыточных давлений от 105 до 109 Па, что значительно шире реального диапазона.
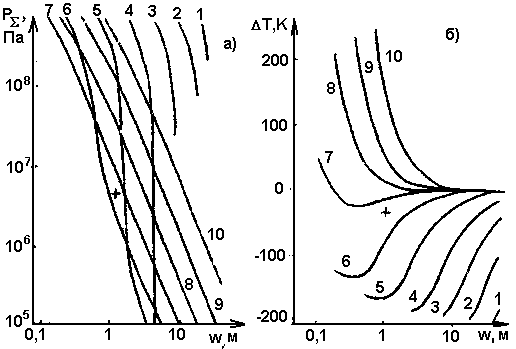
Рис. 2. Зависимость суммарного избыточного давления PS
(a) и суммарного изменения температуры магмы D
T на выходе из дайки (б) от толщины дайки при различных скоростях движения магмы v: 1 - 0,1 мм/с; 2 - 0,4 мм/с; 3 - 1,6 мм/с; 4 - 6,7 мм/с; 5 - 2,7 см/с; 6-11 см/с; 7-45 см/с; 8 - 1,8 м/с; 9 - 7,4 м/с; 10 - 30 м/с (Н = 10 км, Т0 = 1500 К, t = 3 сут).
 |
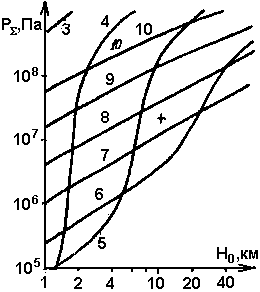 |
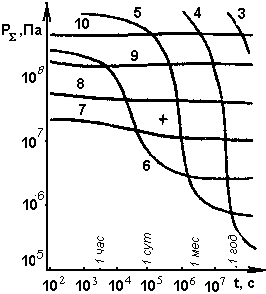
Рис. 3. Зависимость избыточного давления в магматическом очаге от возраста дайки при различных скоростях движения магмы. Параметры и обозначения кривых те же, что на рис. 2 (Н = 10 км, Т0 - 1500 К, W = 1 м). |
Рис. 4. Зависимость суммарного избыточного давления в очаге от глубины его залегания при различных скоростях движения магмы. Параметры и обозначения кривых те же, что на рис. 2 (Т0 = 1500 K,w=lм,t = 3 сут). |
 |
 |
|
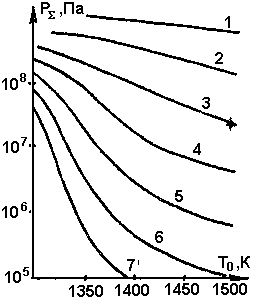
Рис. 5- Зависимость суммарного избыточного давления от начальной температуры магмы в очаге при различных толщинах w дайки: 1-16 см; 2-40 см; 3 ~1м; 4 - 2,5 м; 5 - 6,3 м; 6 - 16 м; 7 - 40 м (v= 1 м/с, Н = 10 км, t = 3 сут) |
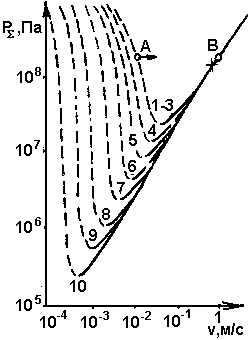
Рис. 6. Зависимость избыточного давления в очаге от скорости движения магмы при различных временах t существования дайки: 1 - 100 с; 2-7,5 мин; 3 - 35,5 мин; 4 - 2 ч 45 мин; 5 - 13 ч; 6 - 58 ч; 7 -11 сут; 8- 51 сут; 9 - 237 сут,. 10 - 3 года (w= 1 м, Т0 = 1500 К, Н = 10 км). Пунктиром обозначены участки нестабильного режима. |
Анализируя кривые рис. 2 — 6, можно выявить следующие качественные закономерности:
1. Величина D
Т немонотонно зависит от w (так же, как, впрочем, и от всех остальных параметров). Однако здесь результирующая величина D
Т в равной мере определяется как суммарным остыванием из-за теплоотдачи, так и суммарным "вязким" разогревом ![]() , который, как видно из этого соотношения, сам зависит от РS
. Это значит, что проще и разумнее анализировать не D
ТS
, а "первичную" функцию РS.
, который, как видно из этого соотношения, сам зависит от РS
. Это значит, что проще и разумнее анализировать не D
ТS
, а "первичную" функцию РS.
2. Величина РS монотонно зависит от w, H, t и Т0, хотя наклон этой зависимости в некоторых случаях меняется весьма прихотливым образом.
3. Единственная переменная, от которой РS зависит немонотонно, - это скорость движения магмы. Кривые РS(v) имеют минимум при любом наборе остальных параметров. Отсюда следует, что далеко не все режимы движения магмы по дайке являются стабильными. А именно, на рис. 6 штриховые участки кривых левее минимума с ![]() соответствуют нестабильному режиму. Действительно, пусть каким-либо образом реализован режим течения, соответствующий точке А на рис. 6. Тогда любое случайное уменьшение давления вызовет увеличение скорости магмы. Этот самоподдерживающийся процесс закончится перескоком в точку В той же кривой, которая уже соответствует стабильному режиму.
соответствуют нестабильному режиму. Действительно, пусть каким-либо образом реализован режим течения, соответствующий точке А на рис. 6. Тогда любое случайное уменьшение давления вызовет увеличение скорости магмы. Этот самоподдерживающийся процесс закончится перескоком в точку В той же кривой, которая уже соответствует стабильному режиму.
Для удобства пользования функциональные зависимости рис. 2—6 желательно представить (хотя бы приближенно) в аналитической форме. Однако элементарными функциями ни одно из семейств, представленных на этих рисунках, выразить нельзя, поэтому остается лишь возможность приближенно описать поведение функций в непосредственной близости от исходной точки.
Первое приближение в задаче такого рода состоит в том, что искомую функцию представляют в виде суперпозиции линейно независимых составляющих, каждая из которых зависит только от одной из независимых переменных. Поскольку наши переменные на графиках изображены в логарифмическом масштабе (исключение составляет линейная шкала Т0, что компенсируется экспоненциальной зависимостью h (Т)), то искать требуемую связь величин будем в виде
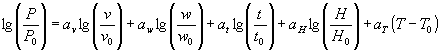
Коэффициенты а для исходной точки, обозначенной на графиках рис. 2-6 крестиком, рассчитываются по наклону соответствующих кривых.
Исходная точка на рис. 2-6 находится в некотором удалении от границы стабильности течения. Интересно было проследить, как изменится функциональная связь параметров при перемещении точки ближе к границе стабильности. Для этого аналогичные расчеты были проведены при координатах точки v0 =0,1 м/с, w0 - 1 м, t0 = 1 мес, Т0 = 1400 К, Н0 = 30 км. Качественный ход кривых оказался почти таким же, как на рис. 2 — 6; однако расчет коэффициентов формулы (7) дал иные результаты.
В табл. 2 представлены результаты расчета для обеих исходных точек.
Таблица 2.
Номер исходной точки |
||
1 |
2 |
|
Параметры исходной точки |
||
V0, м/с |
1 |
0,1 |
W0, м |
1 |
2 |
T0, с |
2,6.105 |
2,6.106 |
H0, км |
10 |
30 |
T0,K |
1500 |
1400 |
Коэффициенты формулы (7) |
||
P0,105 Па |
230 |
174 |
аv |
0,89 |
0,64 |
а<w |
2,01 |
2,35 |
аt |
0,103 |
0,25 |
aH |
0,85 |
1,2 |
aT,K-1 |
0,005 |
0,014 |
Сравнивая величины а в двух столбцах табл. 2, можно сделать такие выводы:
1. При движении магмы в режимах, достаточно удаленных от границы стабильности, избыточное давление в питающем очаге пропорционально глубине залегания очага и скорости магмы (коэффициенты 0,85 и 0,89 достаточно близки к единице), обратно пропорционально квадрату толщины дайки, очень слабо зависит от возраста дайки и довольно сильно - от начальной температуры.
2. По мере приближения к границе стабильности зависимость давления от скорости ослабевает (в ~ 1 ,5 раза), в то же время все остальные параметры начинают влиять на процесс значительно сильнее, чем в режимах, далеких от граничного (температура — втрое сильнее, возраст — в 2,5 раза, глубина - в 1,5 раза, толщина дайки — на 15%).
На рис. 6 режимы стабильного и нестабильного движения легко идентифицируются. На других рисунках этой же серии разделить кривые на такие участки сложнее. Тем не менее задача определения границ стабильности движения магмы по дайке имеет большую практическую ценность, и для ее решения была разработана специальная машинная программа. Идея (по сравнению с первой) состояла в том, что в процессе вычисления РS = f(v) велся поиск точки, в которой производная меняла знак с минуса на плюс (эта точка как раз соответствует минимуму каждой из кривых рис. 2) .
Поскольку в искомой точке фиксируются одновременно два параметра (минимальная скорость стабильного движения и минимальное давление, обеспечивающее это движение), то от пятимерного пространства независимых переменных (v, w, Т, Н, t) мы переходим к четырехмерному (скорость v из независимых переменных переходит в разряд зависимых) .
В процессе расчета были получены семейства кривых
|
|
где vmin и Рmin - скорость магмы и остаточное давление в очаге, при которых дайка "замерзает"; D Т - T(z = Н) - Т0 - изменение температуры магмы за время прохождения дайки. Параметры par1 и раr2 выбираются из семейства четырех независимых переменных w, t, Н и Т0 и изменяются в тех же пределах, что и для первой задачи.
Остановка извержения — явление, гораздо легче поддающееся экспериментальному изучению (если не непосредственному, то хотя бы post factum), поэтому мы приводим не выборочные данные, а все семейства кривых, полученные для исходной точки с параметрами w=300 см, T0= 1400К, Н=10 км, t=105 с. Графики приведены на рис. 7 – 12. Как и на рис. 2 – 6, исходная точка помечена крестиком.
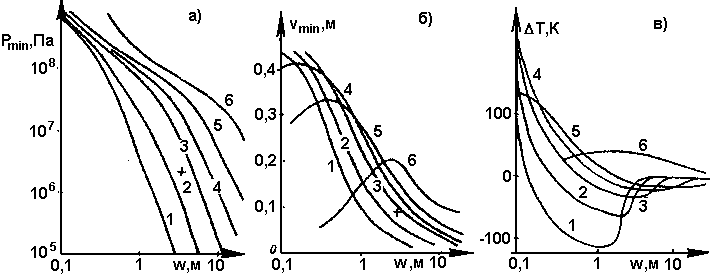
Рис. 7. Зависимость давления Pmin в очаге (а), скорости движения магмы vmin (б) и изменения температуры DТ магмы (в) в замерзающей дайке от толщины дайки при различных начальных температурах Т0 в питающем очаге: 1 – 1500К; 2 – 1434К; 3 – 1367К; 4 – 1344К; 5 – 1322К; 6 – 1300К (Н=10 км, t= 105 с (1 сут).
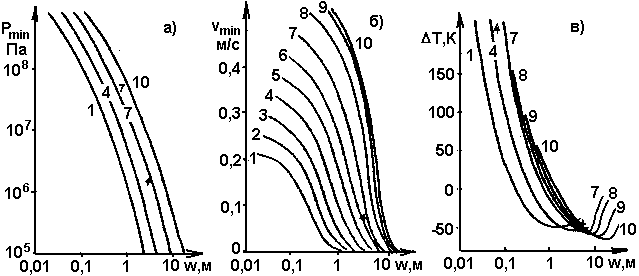
Рис. 8. To же, что на рис. 7, при различных глубинах Н залегания питающего очага: 1 - 1 км; 2 - 1,6 км; 3 - 2,5 км; 4 - 3,9 км; 5 - 6,2 км; 7 - 15,3 км; 8 - 24 км; 9 - 38 км; 10 - 60 км (Т0 = 1400 К, t = 105 с)
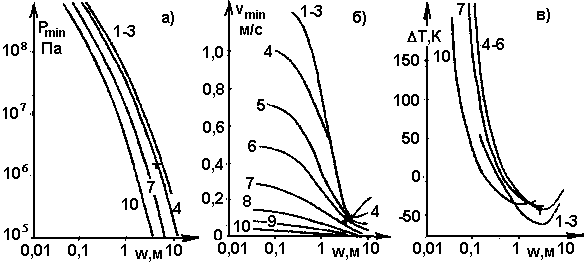
Рис, 9. То же, что на рис 7, при различных временах t существования дайки. Обозначения кривых те же, что на рис. 6 (Т0 = 1400 К, Н = 10 км).
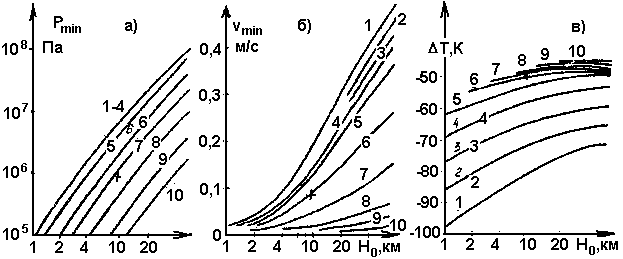
Рис. 10. Зависимость давления Pmin в очаге (а), скорости движения vmin (б) и изменения температуры DТ магмы (в) в замерзающей дайке от глубины залегания Н0 питающего очага при различных временах t существования дайки. Обозначения кривых те же, что на рис. 6 (w = 3 м, Т0= 1400К)
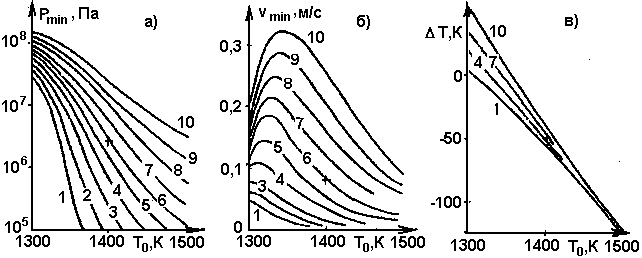
Рис. 11. Зависимость давления Pmin в очаге (а), скорости движения vmin (б) и изменения температуры DТ магмы (в) в замерзающей дайке от температуры Т0 магмы в очаге при различных глубинах Н залегания очага. Обозначения кривых те же, что на рис. 8 (w=3 м, t = 105 с).
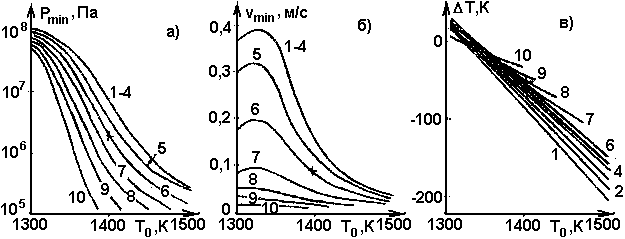
Рис. 12. То же, что на рис. 11, при различных временах t существования дайки. Обозначения кривых те же, что на рис. 6 (w = 3 м, Н = 10 км)
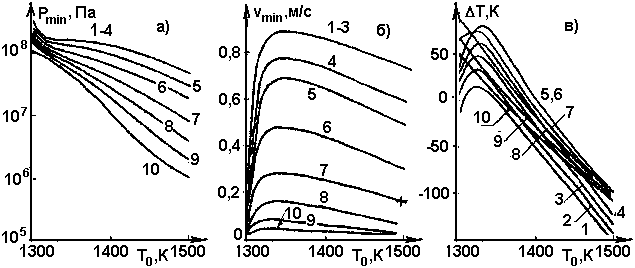
Рис. 13. То же, что на рис. 12, для w = 1 м, Н = 30 км. Обозначения кривых те же. что на рис. 6.
Нетрудно видеть, что функциональные зависимости на этих рисунках ничуть не проще, чем на рис. 2 – 6, поэтому и здесь получить “всеобъемлющую” формулу не удается.
Расчет таких семейств проведен для трех исходных точек. Качественный ход кривых во всех случаях почти неизменен (за исключением, может быть, области минимальных температур Т0). Если записать приближенную зависимость трех анализируемых величин vmin, Pmin и D T от независимых переменных w, t, H и T в форме
|
(8) |
|
(9) |
|
(10) |
то коэффициенты этих формул (справедливых только вблизи соответствующих исходных точек) можно получить тем же способом, что и для первой задачи. Результаты расчета сведены в табл. 3.
Таблица 3.
|
Номер исходной точки |
|||
|
1 |
2 |
3 |
|
|
Параметры исходной точки |
|||
|
w0, |
3 |
1 |
1 |
|
t0, |
105 |
3.105 |
105 |
|
H0, |
10 |
30 |
10 |
|
T0,K |
1400 |
1500 |
1450 |
|
Коэффициенты формулы (8) |
|||
|
v0, м/с |
0,25 |
0,08 |
0,18 |
|
bw |
-27 |
-38 |
-42 |
|
bt |
2,75 |
15,7 |
15,6 |
|
bH |
8,75 |
27,5 |
34 |
|
bT,K-1 |
-0,106 |
-0,1 |
-0,2 |
|
Коэффициенты формулы (9) |
|||
|
P0, 105 Па |
250 |
150 |
120 |
|
сw |
-2,75 |
-2,68 |
-2,8 |
|
сt |
0,21 |
0,41 |
0,23 |
|
cH |
1,85 |
1,56 |
0,94 |
|
cT, K-1 |
-0,017 |
-0,008 |
-0,004 |
|
Коэффициенты формулы (10) |
|||
|
(D T)o, K |
-25 |
-92 |
-70 |
|
dw |
-18* |
-35* |
-60 |
|
dt |
4,6 |
1,32 |
1,5* |
|
dH |
12,4 |
0 |
0 |
|
dT, K-1 |
0,72 |
0,78 |
0,77 |
Примечание. Звездочкой отмечены величины, ошибка определения которых больше 50%.
Анализируя кривые рис 7 – 12 и данные таблицы 3, можно сделать такие выводы:
- Чем холоднее магма в питающем очаге, тем больше давление, при котором замерзает дайка и тем выше скорость магмы в момент замерзания, т.е. тем резче остановка.
- На графиках рис. 7 – 12 часто встречаются участки резкого изменения характера кривых vmin и D T. Почти всегда эти участки соответствуют величинам Pmin>3.108 Па, когда работа сил избыточного давления заметно разогревает магму (в этих случаях D Т всегда существенно больше нуля).
- Интересно отметить очень слабую зависимость D Т от глубины Н залегания питающего очага, а также слабую зависимость D Т от времени существования дайки и температуры магмы в очаге.
- “Выходные” характеристики замерзающей дайки в наибольшей степени зависят от следующих параметров:
D Т – от толщины дайки (при малых толщинах) и в меньшей степени от температуры Т0 в очаге;
Pmin – от толщины дайки (при больших толщинах) и от температуры (при малых Т);
vmin - от толщины дайки (при средних толщинах w~ 1 м) и от времени работы дайки (при w<0,5 м). - Температура магмы на дневной поверхности очень слабо меняется с изменением температуры в очаге (ср., например, величины (Т0 + DТ) для трех исходных точек табл.3).
В процессе анализа семейств кривых для исходных точек 2 и 3 (см. табл. 3) выяснилось, что при почти полной идентичности качественной картины одно из семейств для точки 2 существенно отличается от аналогичных семейств двух других точек. Эта группа кривых приведена на рис. 13. Сравнив рис. 12 и 13, нетрудно убедиться, что в последнем случае Pmin зависит от температуры в несколько раз слабее, чем на рис. 12; в то же время минимальная скорость vmin необычно сильно изменяется при изменении времени существования дайки в диапазоне от ~ 5 мин до ~ 100 ч. Чем вызвано такое изменение хода кривых: изменением толщины дайки (с 3 до 1 м) или изменением глубины залегания питающего очага (с 10 до 30 км)? 0твет на этот вопрос дает анализ соответствующих кривых для точки 3 (w = 1 м, Н = 10 км). Семейства Pmin = j (T0, t) и D Т = y (Т0, t) для точек 2 и 3 практически совпадают, в то время как семейство vmin= f (To, t) занимает некое промежуточное положение между семействами рис. 12,а и 13,а.
Последний факт позволяет предположить, что в четырехмерном пространстве независимых параметров w, t, H и Т0 могут существовать и другие "особые" области, так что проведенный анализ "сечений" этого пространства в трех исходных точках дает лишь ориентировочное представление о форме многомерных функциональных зависимостей vmin= f (w, t, Н, Т0), Pmin = j (w, t, H, T0) и D T = y (w, t, H, T0) в момент "замерзания" дайки. Такой же вывод можно сделать и относительно обсуждавшихся выше режимов стабильного движения магмы по открытой дайке.
В заключение отметим, что проведенный анализ показал важную роль вязкого разогрева магмы как физического процесса, эффективно компенсирующего теплопотери через стенки дайки. Большое количество исходных параметров, определяющих "выходные" характеристики процесса, не позволяют считать настоящий анализ полным и исчерпывающим; однако разработанная методика и программа машинного расчета могут быть легко применены для систематического анализа в любом диапазоне исходных параметров магм и питающих очагов.
Список литературы:
1. Fujii M., Uyeda S. Thermal instabilities during flow of magma in volcanic conditions. - J. Geophysical Research, 1974, v. 79, № 23, p. 3367 - 3369.
2. Федотов С.А. О подъеме основных магм в земной коре и механизме трещинных базальтовых извержений. - Изв. АН СССР, Сер. геол., 1976, № 10, с. 5 - 23.
3. Hardee H.C., Larson D.N. Viscous dissipation effects in magma conduits. - J. Volcanology and Geothermal Research, 1977, v.2, № 3, p. 299 - 308.
4. March B.D. On the cooling of ascending andesitic magmas.— Phil. Trans. Roy. Soc. A, 1976, v. 288, p. 611 - 625.
5. Лебедев Е.Б., Хитаров Н.И. Физические свойства магматических расплавов. М.: Наука, 1979.
6. Мак-Дональд Г.А. Вулканы. М.: Мир, 1975.
7. Магницкий В.А. Внутреннее строение и физика Земли. М.: Недра, 1965.
8. Федотов С.А., Горицкий Ю.А. Тепловой расчет цилиндрических питающих каналов и расхода магмы для вулканов центрального типа. Часть II. — Вулканология и сейсмология, 1980, № 1, с. 3 — 15.
9. Федотов С.А. О вязком нагреве магм и лав при течении, диаметрах астеносферных магматических колонн, скоростях подъема магм и дифференциации магм в них под вулканами островных дуг. - Вулканология и сейсмология, 1979, № 1, с. 5 — 15.
10. Лэмб Г. Гидродинамика. М.: ОГИЗ, 1947.
11. Бэрч Ф. Физика земной коры. — В кн. Земная кора, 1957.
12. Морс Ф.М., Фешбах Г. Методы теоретической физики, т. II, М.: ИЛ, 1960.
Опубликовано в виде Препринта ИАЭ-3470/16, 1981.